STATISTIKA
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
b) Rumus Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Rataan Hitung Gabungan
2. Rumus Modus
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
3. Rumus Median (Nilai Tengah)
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar.
b) Data yang Dikelompokkan
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
4. Rumus Jangkauan ( J )
Selisih antara nilai data terbesar dengan nilai data terkecil.
5. Rumus Simpangan Quartil (Qd)
6. Rumus Simpangan baku ( S )
7. Rumus Simpangan rata – rata (SR)
8. Rumus Ragam (R)
Contoh soal statistika
Tabel 1.1 dibawah ini:
Jawab :
TRIGONOMETRI
Rumus Trigonometri
A. Penggunaan Rumus Sinus dan Cosinus Jumlah Dua Sudut, Selisih Dua Sudut, dan Sudut Ganda
1. Rumus Cosinus Jumlah dan Selisih Dua Sudut
Sebelum membahas rumus trigonometri cosinus untuk jumlah dan selisih dua sudut, perlu kamu ingat kembali dalam segitiga siku-siku ABC berlaku:

Selanjutnya, perhatikanlah gambar berikut.

Dari lingkaran yang berpusat di O(0, 0) dan berjari-jari 1 satuan misalnya,
∠ AOB = ∠ A
∠ BOC = ∠ B
maka ∠AOC = ∠ A + ∠ B
Cartesius, maka:
a. koordinat titik A (1, 0)
b. koordinat titik B (cos A, sin A)
c. koordinat titik C {cos (A + B), sin (A + B)}
d. koordinat titik D {cos (–B), sin (–B)} atau (cos B, –sin B)

Rumus cosinus jumlah dua sudut:
cos (A + B) = cos A cos B – sin A sin B
Dengan cara yang sama, maka:
cos (A – B) = cos (A + (–B))
cos (A – B) = cos A cos (–B) – sin A sin (–B)
cos (A – B) = cos A cos B + sin A sin B
Rumus cosinus selisih dua sudut:
cos (A – B) = cos A cos B + sin A sin B
2. Rumus Sinus Jumlah dan Selisih Dua Sudut
Perhatikan rumus berikut ini.

Maka rumus sinus jumlah dua sudut: sin (A + B) = sin A cos B + cos A sin B
Dengan cara yang sama, maka:
sin (A – B) = sin {A + (–B)}
= sin A cos (–B) + cos A sin (–B)
= sin A cos B – cos A sin B
Rumus sinus selisih dua sudut: sin (A – B) = sin A cos B – cos A sin B
3. Rumus Tangen Jumlah dan Selisih Dua Sudut

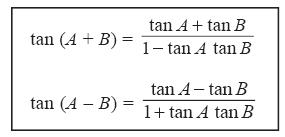
4. Penggunaan Rumus Sinus, Cosinus, dan Tangen Sudut Ganda
Rumus untuk sin 2α
Anda telah mengetahui bahwa
sin (α + β) = sin α cos β + cos α sin β.
Untuk β = α, diperoleh
sin (α + α) = sin α cos α + cos α sin α
sin 2 α = 2 sin α cos α
Jadi, sin 2α = 2 sin α cos α
Rumus untuk cos 2α
Anda juga telah mempelajari bahwa

Rumus untuk tan 2α

Perkalian, Penjumlahan, serta Pengurangan Sinus dan Kosinus
Perkalian Sinus dan Kosinus
Kita telah mempelajari rumus-rumus jumlah dan selisih dua sudut dalam trigonometri, yaitu:


Penjumlahan dan Pengurangan Sinus
Rumus perkalian sinus dan kosinus dalam trigonometri di bagian C.1 dapat
ditulis dalam rumus berikut.

Identitas Trigonometri

Contoh Soal Trigonometri






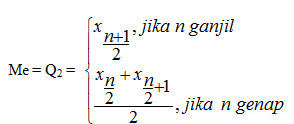

















Post a Comment